Als letzten Schritt in unserem Quantencomputer messen wir nun den
gewonnen Zustand unseres Systems (eigentlich würde es genügen,
![]() zu messen, wir messen aber jetzt
zu messen, wir messen aber jetzt ![]() und
und
![]() ), und rechnen danach klassisch weiter.
), und rechnen danach klassisch weiter.
Die diskrete Fouriertransformation wird bei diesem Algorithmus dazu
benötigt, die Periode im Funktionsgraphen der modularen Exponentation
zu ermitteln, die unserer gesuchten Ordnung ![]() entspricht. Dabei wird
praktisch der ,,Offset``
entspricht. Dabei wird
praktisch der ,,Offset`` ![]() eines erhaltenen Wertes
eines erhaltenen Wertes ![]() ausgelöscht und die Periode finden wir in der gemessenen Amplitude
wieder (allerdings als Kehrwert und mit einem Faktor versehen),
zusätzlich tritt eine Phasenverschiebung auf, da wir aber sowieso nur
die Amplitude messen, können wir diese ignorieren.
ausgelöscht und die Periode finden wir in der gemessenen Amplitude
wieder (allerdings als Kehrwert und mit einem Faktor versehen),
zusätzlich tritt eine Phasenverschiebung auf, da wir aber sowieso nur
die Amplitude messen, können wir diese ignorieren.
Die Wahrscheinlichkeit, einen bestimmten Zustand ![]() und
und
![]() (
(![]() ) zu beobachten, beträgt:
) zu beobachten, beträgt:
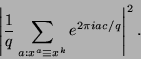 |
(17) |
Da ![]() nun aber die Ordnung
nun aber die Ordnung ![]() besitzt, können wir diese Summe
umschreiben, indem wir
besitzt, können wir diese Summe
umschreiben, indem wir ![]() setzen und erhalten:
setzen und erhalten:
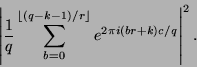 |
(18) |
Wir können nun
![]() ausklammern und
ausklammern und ![]() durch
durch ![]() ersetzen, wobei dieser Rest noch so ,,verschoben``
wird, daß er im Intervall
ersetzen, wobei dieser Rest noch so ,,verschoben``
wird, daß er im Intervall ![]() liegt, wir schreiben dafür
liegt, wir schreiben dafür
![]() und erhalten
und erhalten
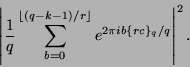 |
(19) |
Die Summe können wir nun als Integral schreiben ([Heu98] Eulersche Summenformel) und gewinnen daraus
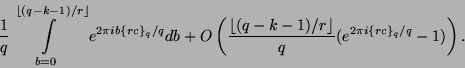 |
(20) |
Wenn
![]() (dies ist unabhängig von
(dies ist unabhängig von ![]() !) ist obiger
Fehlerterm durch
!) ist obiger
Fehlerterm durch ![]() beschränkt und das Integral, also die
Wahrscheinlichkeit den Zustand
beschränkt und das Integral, also die
Wahrscheinlichkeit den Zustand
![]() zu messen, ist
groß. Dies kann man sich z.B. am komplexen Einheitskreis
veranschaulichen, falls die einzelnen Amplituden ungefähr in die gleiche
Richtung ,,zeigen``, ergibt sich eine Verstärkung.
zu messen, ist
groß. Dies kann man sich z.B. am komplexen Einheitskreis
veranschaulichen, falls die einzelnen Amplituden ungefähr in die gleiche
Richtung ,,zeigen``, ergibt sich eine Verstärkung.
Wenn wir nun in dem Integral ![]() substituieren, erhalten wir
substituieren, erhalten wir
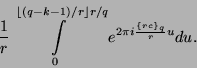 |
(21) |
Nun können wir, da ![]() , mit einem Fehler von nur
, mit einem Fehler von nur ![]() die
obere Grenze des Integrals durch
die
obere Grenze des Integrals durch ![]() ersetzen und bekommen
ersetzen und bekommen
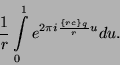 |
(22) |
![]() ist im Intervall
ist im Intervall
![]() , der
Betrag des Integral wird also für
, der
Betrag des Integral wird also für
![]() minimal und beträgt
minimal und beträgt ![]() . Der Betrag dieser Größe ist eine
untere Schranke für die Wahrscheinlichkeit, einen bestimmten Zustand
mit
. Der Betrag dieser Größe ist eine
untere Schranke für die Wahrscheinlichkeit, einen bestimmten Zustand
mit
![]() zu beobachten, deswegen ist diese
asymptotisch durch
zu beobachten, deswegen ist diese
asymptotisch durch ![]() beschränkt und für genügend
große
beschränkt und für genügend
große ![]() mindestens
mindestens ![]() .
.
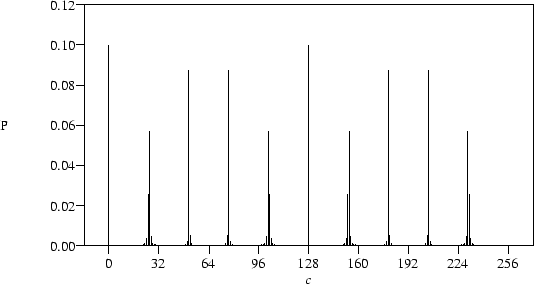 |
Die Wahrscheinlichkeit
![]() zu messen, beträgt also
mindestens
zu messen, beträgt also
mindestens ![]() , falls
, falls
| (23) |
| (24) |
Daraus erhalten wir:
| (25) |
wobei wir ![]() und
und ![]() kennen.
kennen.
Würde ![]() nun
nun ![]() teilen, erhielten wir somit direkt unsere gesuchte
Ordnung
teilen, erhielten wir somit direkt unsere gesuchte
Ordnung ![]() . Dies ist allerdings im allgemeinen nicht der Fall, wir
können aber über einen kleinen Umweg trotzdem
. Dies ist allerdings im allgemeinen nicht der Fall, wir
können aber über einen kleinen Umweg trotzdem ![]() ermitteln, indem
wir die sogenannte Kettenbruchentwicklung anwenden.
ermitteln, indem
wir die sogenannte Kettenbruchentwicklung anwenden.
Da zu Beginn ![]() gewählt wurde, gibt es höchstens einen Bruch
gewählt wurde, gibt es höchstens einen Bruch
![]() mit
mit ![]() , der obige Bedingung erfüllt. Wir erhalten diesen
Bruch vollständig gekürzt, indem wir
, der obige Bedingung erfüllt. Wir erhalten diesen
Bruch vollständig gekürzt, indem wir ![]() auf den nächsten Bruch
runden, der einen Nenner kleiner als
auf den nächsten Bruch
runden, der einen Nenner kleiner als ![]() hat. Dieser Bruch kann
mittels Kettenbruchentwicklung von
hat. Dieser Bruch kann
mittels Kettenbruchentwicklung von ![]() effizient gefunden werden.
effizient gefunden werden.
Ein (endlicher, einfacher) Kettenbruch ist ein Ausdruck der Form
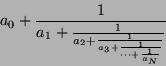 |
(26) |
mit
![]() . Jede positive rationale Zahl
kann durch einen Kettenbruch dargestellt werden, der wie folgt
berechnet wird: Sei
. Jede positive rationale Zahl
kann durch einen Kettenbruch dargestellt werden, der wie folgt
berechnet wird: Sei
![]() und
und
![]() für ein
für ein
![]() . Wenn
. Wenn ![]() dann sei
dann sei
![]() und
und
![]() für ein
für ein
![]() usw. Bei rationalem
usw. Bei rationalem ![]() terminiert dieser Prozeß und wir
erhalten die
terminiert dieser Prozeß und wir
erhalten die ![]() der Kettenbruchentwicklung (vgl. [EJ94],
[Knu97] Analyse des Euklidischen Algorithmus).
der Kettenbruchentwicklung (vgl. [EJ94],
[Knu97] Analyse des Euklidischen Algorithmus).
Ist ![]() nun teilerfremd zu
nun teilerfremd zu ![]() , erhalten wir damit
, erhalten wir damit ![]() (wir bekommen
durch die Kettenbruchentwicklung einen vollständig gekürzten
Bruch). Es gibt
(wir bekommen
durch die Kettenbruchentwicklung einen vollständig gekürzten
Bruch). Es gibt ![]() mögliche Werte von
mögliche Werte von ![]() teilerfremd zu
teilerfremd zu ![]() (
(
![]() ist die Eulersche
ist die Eulersche ![]() -Funktion, die die Anzahl der zu
-Funktion, die die Anzahl der zu ![]() teilerfremden Zahlen angibt). Jeder dieser Brüche
teilerfremden Zahlen angibt). Jeder dieser Brüche ![]() ist nahe an
einem Bruch
ist nahe an
einem Bruch ![]() mit
mit
![]() . Es gibt zudem r mögliche
Werte für
. Es gibt zudem r mögliche
Werte für ![]() , da
, da ![]() die Ordnung von
die Ordnung von ![]() ist.
ist.
Da jeder dieser Zustände mit einer Wahrscheinlichkeit von mindestens
![]() auftritt, erhalten wir
auftritt, erhalten wir ![]() mit einer Wahrscheinlichkeit
größer oder gleich
mit einer Wahrscheinlichkeit
größer oder gleich ![]() . Wenn wir nun ausnutzen, daß
. Wenn wir nun ausnutzen, daß
![]() für eine Konstante
für eine Konstante ![]() ist
(siehe [HW79], zitiert in [Sho97] und [EJ94]),
müssen wir das Experiment also nur
ist
(siehe [HW79], zitiert in [Sho97] und [EJ94]),
müssen wir das Experiment also nur
![]() mal wiederholen,
um
mal wiederholen,
um ![]() mit einer hohen Wahrscheinlichkeit zu erhalten.
mit einer hohen Wahrscheinlichkeit zu erhalten.
Dies kann in der Praxis noch weiter verbessert werden, indem bei
gemessenem ![]() auch noch Zahlen nahe an
auch noch Zahlen nahe an ![]() wie
wie
![]() ausprobiert werden, da auch diese noch eine einigermaßen
hohe Wahrscheinlichkeit haben, nahe an einem Bruch
ausprobiert werden, da auch diese noch eine einigermaßen
hohe Wahrscheinlichkeit haben, nahe an einem Bruch ![]() zu sein.
zu sein.
Außerdem kann man die Rechnung nicht nur mit einem Kandidaten ![]() für
für ![]() , sondern, da der Bruch
, sondern, da der Bruch ![]() ja vollständig gekürzt zu
ja vollständig gekürzt zu
![]() vorliegt, auch für
vorliegt, auch für
![]() durchführen, ob diese
Werte vielleicht die Ordnung von
durchführen, ob diese
Werte vielleicht die Ordnung von ![]() sind. Weiterhin ist es auch noch
möglich, daß man, wenn man zwei Kandidaten für
sind. Weiterhin ist es auch noch
möglich, daß man, wenn man zwei Kandidaten für ![]() gefunden hat,
das kleinste gemeinsame Vielfache dieser beiden Werte ausprobiert,
auch dadurch lassen sich die Versuche auf dem Quantencomputer
reduzieren, so daß man zwar mehr klassische Nachbearbeitung braucht,
aber der schwierig zu realisierende Quantencomputer nur wirklich da
eingesetzt wird, wo er unbedingt benötigt wird.
gefunden hat,
das kleinste gemeinsame Vielfache dieser beiden Werte ausprobiert,
auch dadurch lassen sich die Versuche auf dem Quantencomputer
reduzieren, so daß man zwar mehr klassische Nachbearbeitung braucht,
aber der schwierig zu realisierende Quantencomputer nur wirklich da
eingesetzt wird, wo er unbedingt benötigt wird.